对Photoshop高斯含糊滤镜的算法总结
时间:2023/7/9作者:未知来源:手揣网教程人气:
- [摘要]最近有感于部分网友对高斯模糊滤镜的研究,现总结如下。高斯模糊是数字图像模板处理法的一种。其模板是根据二维正态分布(高斯分布)函数计算出来的。 正态分布最早由A.棣莫弗在求二项分布的渐...最近有感于部分网友对高斯模糊滤镜的研究,现总结如下。高斯模糊是数字图像模板处理法的一种。其模板是根据二维正态分布(高斯分布)函数计算出来的。
正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。故名高斯模糊。一维正态分布的函数定义:
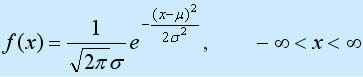
型随机变量的分布,第一参数μ是遵从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差,所以正态分布记作N(μ,σ2 )。 遵从正态分布的随机变量的概率规律为取 μ邻近的值的概率大 ,而取离μ越远的值的概率越小;σ越小,分布越集中在μ附近,σ越大,分布越分散。正态分布的密度函数的特点是:关于μ对称,在μ处达到最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点。它的形状是中间高两边低 ,图像是一条位于x轴上方的钟形曲线。当μ=0,σ2 =1时,称为标准正态分布,记为N(0,1)。
两个常数的意义:μ-期望,σ^2 方差。
下面我们解决第一个疑问:高斯模糊滤镜中的半径是什么?答案是高斯半径就是公式中的σ。
高斯曲线的图形和半径的含义如下图(来自Adobe SDK中技术支持专家的文档)所示:
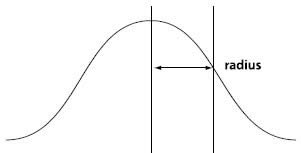
可见高斯半径(σ)对曲线形状的影响,σ越小,曲线越高越尖,σ越大,曲线越低越平缓。对二维图像来说,是一个钟形曲面,高斯半径越小,曲面越高越尖越陡峭;高斯半径越大,曲面越低越平缓。因此高斯半径越小,则模糊越小,高斯半径越大,则模糊程度越大。我们将看到ps对高斯半径的范围定义是【0.1~250】。当半径为0.1时,高斯模板在计算后只有中间像素为1,其他像素均=0(实际上只是趋近0),即图像不会有变化。
第二个疑问,高斯模板大小和高斯半径的关系?这是一个一直困扰我们的误解。因为我们的思维进入了物理实现的误区。在物理实现中,高斯模板有界,从而使我们忽略了这个问题的真正答案:高斯模板在逻辑上是无边界的。也就是说高斯模板本质上是逻辑上无穷拓展曲面的一个近似。因此,模板大小我们应该认为它是无穷大的。只不过在计算的时候,因为在远处趋近0,因此在某个阈值之下我们不再考虑这些值,这个阈值就是模板边界。
下面,二维高斯曲面的公式(x,y代表像素的模板坐标,模板中心位置为原点):
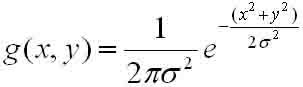
即:g(x,y)= ( 1 / (2*pi*σ^2) ) * exp( -(x^2+y^2)/(2*σ^2) ) ;根据这个公式,我们可以计算出不同半径下的高斯模板,实际上模板是无穷大的,只是在中心较远处,他们会趋近0.例如,我们计算出r=0.7时的一个归一化后的高斯模板:
高斯模板(guass radius=0.700000)
在网络上众所周知流传的高斯3*3模板实际上是对高斯曲面的一个整数除法形式的近似:
1 2 1
2 4 2 /16
1 2 1
实际验证,我们发现这个3*3模板实际上是对高斯半径约为0.849时的一个近似,当r=0.849时,其3*3归一模板为(在MATLAB中,输入h=fspecial('gaussian', 3, 0.849);即可得到这个模板):
(guass radius=0.849000)
0.062467 0.125000 0.062467
0.125000 0.250131 0.125000
0.062467 0.125000 0.062467然后我们可以用Matlab中的imfilter来对图像进行高斯模糊的处理:
img = imread('c:\demo.bmp');
h = fspecial('gaussian', 3, 0.849);
img2 = imfilter(img, h);
subplot(121), imshow(img); title('原图')
subplot(122), imshow(img2); title('高斯模糊后')效果如下:
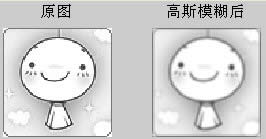
我们可以在Matlab中用如下语句绘制高斯曲面:
绘制高斯曲面的Matlab代码
效果如下图:
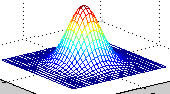
在数字信号处理中,高斯模糊算法是一种滤波器,它的时域和频域曲线如下所示:
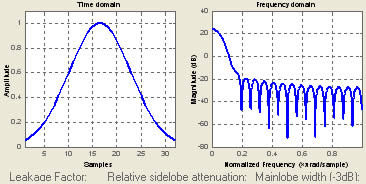
从频域曲线看出,高斯模糊本质上一种低通滤波器。体现在图像处理上,图像的边缘等灰度变化剧烈的地方对应高频信息,将被滤除。
最后,我们给出计算高斯模糊模板的C语言代码,请注意,由于高斯模板是对称的,实际上我们只需要计算出大约1/4模板即可。但这里的代码我们没有做这样的优化。我们输出的模板是(2*N+1)*(2N+1),高斯半径用r表示。
计算高斯模板
同时,作为比较,我们给出在Matlab中生成高斯模板的代码(fspecial的代码局部,其中p3是第三个参数即高斯半径):
case 'gaussian' % Gaussian filter siz = (p2-1)/2; %注:p2即模板边长,默认值为33 std = p3; %注:p3即高斯半径,默认为为0.5 [x,y] = meshgrid(-siz(2):siz(2),-siz(1):siz(1)); arg = -(x.*x + y.*y)/(2*std*std); h = exp(arg); h(h<eps*max(h(:))) = 0; sumh = sum(h(:)); %注:模板归一化 if sumh ~= 0, h = h/sumh; end;更多对Photoshop高斯模糊滤镜的算法总结相关文章请关注PHP中文网!
Photoshop默认保存的文件格式,可以保留所有有图层、色版、通道、蒙版、路径、未栅格化文字以及图层样式等。
关键词:对Photoshop高斯含糊滤镜的算法总结